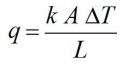You are here
Every material used in an envelope assembly has fundamental physical properties that determine their energy performance like conductivity, resistance, and thermal mass. Understanding these intrinsic properties will help you chose the right materials to manage heat flows.
Thermal Conductivity (k)
A material’s ability to conduct heat.
 |
Each material has a characteristic rate at which heat will flow through it. The faster heat flows through a material, the more conductive it is. Conductivity (k) is a material property given for homogeneous solids under steady state conditions.
It is used in the follow equation:
Units for conductivity
Imperial – BTU*in/h ft ºF: In the Imperial system, conductivity is the number of British thermal units per hour (Btu/h) that flow through 1 square foot (ft2) of material that is 1 in. thick when the temperature difference across that material is 1ºF (under conditions of steady heat flow).
SI - W/m ºC or W/m K: The System International (SI) equivalent is the number of watts that flow through 1 square meter (m2) of material that is 1 m thick when the temperature difference across that material is 1 K (equal to 1ºC) under conditions of steady heat flow.
Thermal Conductance (C)
Conductivity per unit area for a specified thickness. Used for standard building materials.
In basic building materials, heat flow is usually measured by conductance (C), not conductivity. Conductance is a material's conductivity per unit area for the object's thickness (in units of W/m²K for metric and BTU/hr•ft2•°F for Imperial).
Conductance is an object property and depends on both the material and its thickness. Many solid building materials such as common brick, wood siding, batt or board insulation, and gypsum board are widely available in standard thicknesses and compositions. For such common materials, it is useful to know the rate of heat flow for that standard thickness instead of the rate per inch.
U-Factor (U)
Overall conductance of a building element. Used for layered building assemblies.
In layered assemblies, conductances are combined into a single number called the "U-factor" (or sometimes the “U-value”).
| U-factor and conductance translate conductivity from a material property to an object property. |
U is the overall coefficient of thermal transmittance, expressed in terms of Btu/h ft2 ºF (in SI units, W/m2 K). This is the same unit as conductance because it’s a measure of the same thing: conductance is used for a specific material, U-factor is used for a specific assembly. Lower U-factors mean less conduction, which means better insulation.
For instance, the overall U-factor of a window includes the conductances of the glass panes, the air inside, the framing material, and any other materials in their different thicknesses and locations. Except in special cases, the conductances of the materials cannot be added to determine U-factor of the assembly.
The U-factor is an overall coefficient of heat transfer, and includes the effects of all elements in an assembly and all sensible modes of heat transfer (conduction, convection, and radiation), but not latent heat transfer (moisture related).
The term U-factor should be used only where heat flow is from air on the outside of the envelope, through the envelope assembly to air on the inside. It should not be used on basement walls, for example.
Thermal Resistance (R-value = 1/U)
A material’s ability to resist heat flow.
Designated as R (R-value), thermal resistance indicates how effective any material is as an insulator.
The reciprocal of thermal conductance, R is measured in hours needed for 1 Btu to flow through 1 ft2 of a given thickness of a material when the temperature difference is 1ºF. In the Imperial system, the units are ft2•°F•hr/BTU. SI units are m²K/W.
Thermal resistance values are sometimes tabulated for both unit thicknesses and for a sample of material with a known thickness. For example, the resistance of pine may be given as 1.0 ft2•°F•hr/BTU per inch, or values may be tabulated for a 2x6 pine stud as 5.5 ft2•°F•hr/BTU. For a homogeneous material such as wood, doubling the thickness will double the R-value. R-values are not typically specified for assemblies of materials. U-factors are used for assemblies.
Insulation, which prevents heat flow through the building envelope, is often measured by its R-value. A higher R‐value indicates a better insulating performance. When looking at spec sheets, be sure you are reading the R-value in the right units, as the units are not always explicitly written.
For more information on designing with insulation – including a table of common R-values, thermal bridging, and how to calculate overall R-values for assemblies, see the Insulation page.
Using U-factors and R-values in practice
The variety of terms used so far to express thermal properties is potentially bewildering. When dealing with complex layered building constructions, it’s useful to combine thermal properties into a single overall number for specifying envelope design criteria.
For the total building envelope, this is often expressed as a U-factor. That said, windows are often expressed with U-factor and walls are often expressed with R-values. There is no strict rule.
Calculating the overall U-factor starts with adding resistances. U-factors are calculated for a particular element (roof, wall, etc.) by finding the resistance of each constituent part, including air films and air spaces, and then adding these resistances to obtain a total resistance. The U-factor is the reciprocal of this sum (Σ) of resistances: U= 1/ Σ R.
For more information on how to use R-values and U-factors for envelope design, see the page on Total R-value and thermal bridging.
Thermal Mass
Thermal mass is a material's resistance to change in temperature as heat is added or removed, and is a key factor in dynamic heat transfer interactions within a building. The four factors to understand are: density, specific heat, thermal capacity, and thermal lag.
Density
Dense materials usually store more heat.
Density is the mass of a material per unit volume. In the Imperial system, density is given as lb/ft3; in the SI system, it is given as kg/m3. For a fixed volume of material, greater density will permit the storage of more heat.
Specific Heat
High specific heat requires a lot of energy to change the temperature.
Specific heat is a measure of the amount of heat required to raise the temperature of given mass of material by 1º. In the Imperial system, this is expressed as Btu/lb ºF; in the SI system, it is expressed as kJ/kg K. It takes less energy input to raise the temperature of a low-specific-heat material than that of a high-specific-heat material.
For instance, one gram of water requires one calorie of heat energy to rise one degree Celsius in temperature. Water has a high heat capacity and, therefore, is sometimes used as thermal mass in buildings.
| Material |
Heat capacity J/(g·K) |
| Brick | 0.84 |
| Concrete | 0.88 |
| Granite | 0.79 |
| Gypsum | 1.09 |
| Soil | 0.80 |
| Wood | 1.2-2.3 |
| Water | 4.2 |
Thermal Capacity (Thermal Mass)
Density x Specific Heat = How much heat can be stored per unit volume
Thermal capacity is an indicator of the ability of a material to store heat per unit volume. The greater the thermal capacity of a material, the more heat it can store in a given volume per degree of temperature increase. Thermal capacity for a material is obtained by taking the product of density and specific heat. Units are J/K.
Higher thermal capacity can (but will not always) reduce heat flow from the outside to the inside environment by storing the heat within the material. Heat entering a wall construction during the daytime, for example, can be stored within the wall for several hours until it flows back out to the cool night air—assuming appropriate weather conditions and adequate thermal capacity.
Thermal Lag (Time Lag)
With high thermal mass, it can take hours for heat to flow from one side of the envelope to the other.
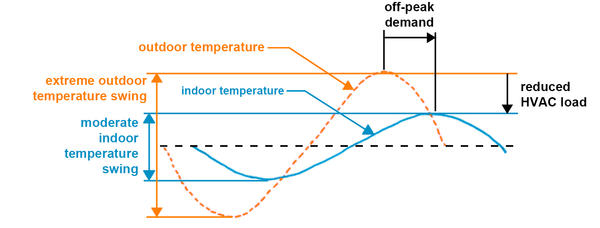
This slowing of the flow of heat is called "thermal lag" (or time lag), and is measured as the time difference between peak temperature on the outside surface of a building element and the peak temperature on the inside surface. Some materials, like glass, do not have much of a thermal lag. But the thermal lag can be as long as eight or nine hours for constructions with high thermal mass like double-brick or rammed earth walls.
 |
|
Lag-time and moderation of temperatures due to thermal mass |
As an example, if the sun comes out from behind clouds and strikes a building envelope with high thermal capacity at 10AM, the exterior surface temperature will rise quickly. It may be several hours, however, before this temperature “spike” is seen at the inside surface of the wall. The reason is that some heat is being stored in the wall material. This heat is stored in the wall material until it has absorbed as much as it can (saturated). Heat will then flow to the inside, based on the conductivity of the material.
One example of a thermal lag on a large scale is the fact that the hottest months in most parts of the northern hemisphere are July or August, even though the strongest sun of the year is in June.
Glazing Properties
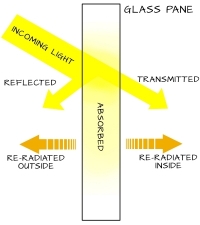 |
| Heat transmission and radiation from a window |
In transparent surfaces, there’s even more to take into account.
Heat transfer through a window involves all three modes of heat transfer; conduction, convection, and radiation. The dominant mode of heat transfer is always changing and depends on the time, the ambient and interior temperatures, the exterior wind speed, and the amount and angle of solar radiation that strikes the window. The insulation capabilities of windows are usually measured by their U-factors; see the table on the Glazing Properties page. The U-factor for a window is primarily a metric used to calculate the conductive portion of the heat transfer through the window.
Because windows (“glazing”) let light and radiation through, there are a host of properties that must be considered to optimize their thermal and visual performance. For example, a simplified metric used to specify radiant heat transfer through the window when solar energy strikes the window is called the solar heat gain coefficient (SHGC). The SHGC is a value between 0 – 1.0 and is a measure of how much radiant heat transfer will occur relative to an unglazed opening.
See more on Glazing Properties
Links and References
- A series of pages that describe the thermal properties of building envelopes - like insulation, resistance, conductivity, and thermal mass.